Distancia de un punto a una recta

07 Nov

Distancia de un punto a una recta

La fórmula para calcular la mínima distancia medida desde el punto hasta la recta \hspace{0.25em} $\ell:\hspace{0.25em} A\,x + B\,y + C = 0$ , es:

$\begin{equation*} D_{P\ell} = \frac{|A\,x_1 + B\,y_1 + C|}{\sqrt{A^2 + B^2}} \end{equation*}$

Obviamente, suponemos que el punto en cuestión no está sobre la recta, porque en ese caso, la distancia buscada es cero.

Observa que si el punto está sobre la recta, entonces satisface su ecuación y como su ecuación, tanto en forma general como en forma normal, están igualadas a cero, al sustituir las coordenadas del punto en la ecuación de la recta en forma normal (que corresponde a fórmula para calcular la distancia de un punto a una recta) obtenemos cero:

$\begin{equation*} \frac{A}{\sqrt{A^2 + B^2}}\,x + \frac{B}{\sqrt{A^2 + B^2}}\,\,y + \frac{C}{\sqrt{A^2 + B^2}} = 0 \end{equation*}$

Ejemplo 1

Calcula la distancia desde la recta $5\,x - 12\,y - 10 = 0$ hasta el punto .

Sustituimos los datos conocidos en la fórmula:

$\begin{eqnarray*} D &=& \frac{|\textcolor{blue}{A}\,\textcolor{red}{x_1} + \textcolor{blue}{B}\,\textcolor{red}{y_1} + \textcolor{blue}{C}|}{\sqrt{\textcolor{blue}{A}^2 + \textcolor{blue}{B}^2}}\\ &=& \frac{|\textcolor{blue}{5}\,(\textcolor{red}{4}) - \textcolor{blue}{12}\,(\textcolor{red}{3}) - \textcolor{blue}{10}|}{\sqrt{\textcolor{blue}{5}^2 + \textcolor{blue}{12}^2}} = \frac{|20 - 36 - 10|}{\sqrt{25 + 144}}\\ &=& \frac{|26|}{\sqrt{169}} = \frac{26}{13} = 2 \end{eqnarray*}$

Curso para terminar tu tesis

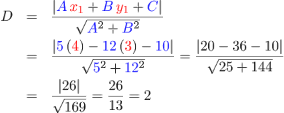
Entonces, desde la recta $5\,x - 12\,y - 10 = 0$ hasta el punto hay 2 unidades de distancia.

Ejemplo 2

¿A qué distancia pasa la recta $3\,x + 4\,y + 15 = 0$ del origen?

Este problema es equivalente a la siguiente solicitud:

Calcula la distancia desde la recta $3\,x + 4\,y + 15 = 0$ hasta el punto .

Ahora que conocemos los datos, basta sustituir en la fórmula de distancia de un punto a una recta y realizar las operaciones que quedan indicadas:

$\begin{eqnarray*} D &=& \frac{|\textcolor{blue}{A}\,\textcolor{red}{x_1} + \textcolor{blue}{B}\,\textcolor{red}{y_1} + \textcolor{blue}{C}|}{\sqrt{\textcolor{blue}{A}^2 + \textcolor{blue}{B}^2}}\\ &=& \frac{|\textcolor{blue}{3}\,(\textcolor{red}{0}) - \textcolor{blue}{4}\,(\textcolor{red}{0}) + \textcolor{blue}{15}|}{\sqrt{\textcolor{blue}{3}^2 + \textcolor{blue}{4}^2}} = \frac{|0 - 0 + 15|}{\sqrt{25}}\\ &=& \frac{|15|}{5} = 3 \end{eqnarray*}$

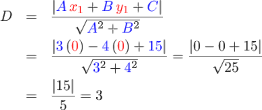
Entonces, la recta pasa a 3 unidades del origen. Para graficar la recta podemos transformarla a la forma simétrica:

$\begin{eqnarray*} 3\,x + 4\,y + 15 &=& 0 \\ 3\,x + 4\,y &=& -15 \\ \frac{3\,x}{-15} + \frac{4\,y}{-15} &=& \frac{-15}{-15}\\ \frac{x}{-5} + \frac{y}{-15/4} &=& 1 \end{eqnarray*}$

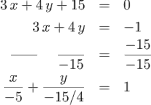
Ahora podemos graficar la recta y mostrar que la distancia al origen es de 3 unidades:

Rendered by QuickLaTeX.com

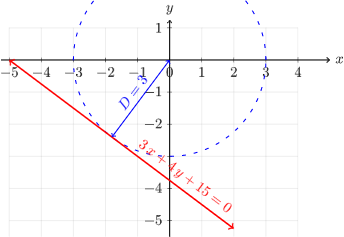
La fórmula para encontrar la distancia de un punto a una recta tiene muchas aplicaciones, sobre todo en problemas de lugar geométrico.

En la siguiente unidad vamos a encontrar el lugar geométrico del punto que se mueve de tal manera que su distancia a una recta es igual a la distancia a otro punto que no se encuentra sobre la recta.

Los problemas que podemos resolver con esta fórmula son muy diversos.

Comentarios